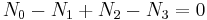Convex regular 4-polytope

In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids (in three dimensions) and the regular polygons (in two dimensions).

These polytopes were first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. Schläfli discovered that there are precisely six such figures. Five of these may be thought of as higher dimensional analogs of the Platonic solids. There is one additional figure (the 24-cell) which has no three-dimensional equivalent.

Each convex regular 4-polytope is bounded by a set of 3-dimensional cells which are all Platonic solids of the same type and size. These are fitted together along their respective faces in a regular fashion.

Contents

Properties

The following tables lists some properties of the six convex regular 4-dimensional polytopes. The symmetry groups of these polytopes are all Coxeter groups and given in the notation described in that article. The number following the name of the group is the order of the group.

Names Family Schläfli
symbol		 Vertices Edges Faces Cells Vertex figures Dual polytope Symmetry group
5-cell
pentatope
hyperpyramid
hypertetrahedron
4-simplex		 simplex
(n-simplex)		 {3,3,3} 5 10 10
triangles		 5
tetrahedra		 tetrahedra (self-dual) A4 120
8-cell
Tesseract
hypercube
4-cube		 hypercube
(n-cube)		 {4,3,3} 16 32 24
squares		 8
cubes		 tetrahedra 16-cell B4 384
16-cell
orthoplex
hyperoctahedron
4-orthoplex		 cross-polytope
(n-orthoplex)		 {3,3,4} 8 24 32
triangles		 16
tetrahedra		 octahedra tesseract B4 384
24-cell
octaplex
polyoctahedron		 {3,4,3} 24 96 96
triangles		 24
octahedra		 cubes (self-dual) F4 1152
120-cell
dodecaplex
hyperdodecahedron
polydodecahedron		 {5,3,3} 600 1200 720
pentagons		 120
dodecahedra		 tetrahedra 600-cell H4 14400
600-cell
tetraplex
hypericosahedron
polytetrahedron		 {3,3,5} 120 720 1200
triangles		 600
tetrahedra		 icosahedra 120-cell H4 14400

Since the boundaries of each of these figures is topologically equivalent to a 3-sphere, whose Euler characteristic is zero, we have the 4-dimensional analog of Euler's polyhedral formula:

N_0 - N_1 %2B N_2 - N_3 = 0\,

where Nk denotes the number of k-faces in the polytope (a vertex is a 0-face, an edge is a 1-face, etc.).

Visualizations

The following table shows some 2 dimensional projections of these polytopes. Various other visualizations can be found in the external links below. The Coxeter-Dynkin diagram graphs are also given below the Schläfli symbol.

5-cell 8-cell 16-cell 24-cell 120-cell 600-cell
{3,3,3} {4,3,3} {3,3,4} {3,4,3} {5,3,3} {3,3,5}
Wireframe orthographic projections inside Petrie polygons.
Solid orthographic projections

tetrahedral
envelope
(cell/vertex-centered)
cubic envelope
(cell-centered)
Cubic envelope
(cell-centered)
cuboctahedral
envelope
(cell-centered)
truncated rhombic
triacontahedron
envelope
(cell-centered)
Pentakis icosidodecahedral
envelope
(vertex-centered)
Wireframe Schlegel diagrams (Perspective projection)

(Cell-centered)
(Cell-centered)
(Cell-centered)
(Cell-centered)
(Cell-centered)
(Vertex-centered)
Wireframe stereographic projections (Hyperspherical)

See also

References

External links

Convex regular 4-polytopes
5-cell 8-cell 16-cell 24-cell 120-cell 600-cell

{3,3,3}
pentachoron

{4,3,3}
tesseract

{3,3,4}
hexadecachoron

{3,4,3}
icositetrachoron

{5,3,3}
hecatonicosachoron

{3,3,5}
hexacosichoron